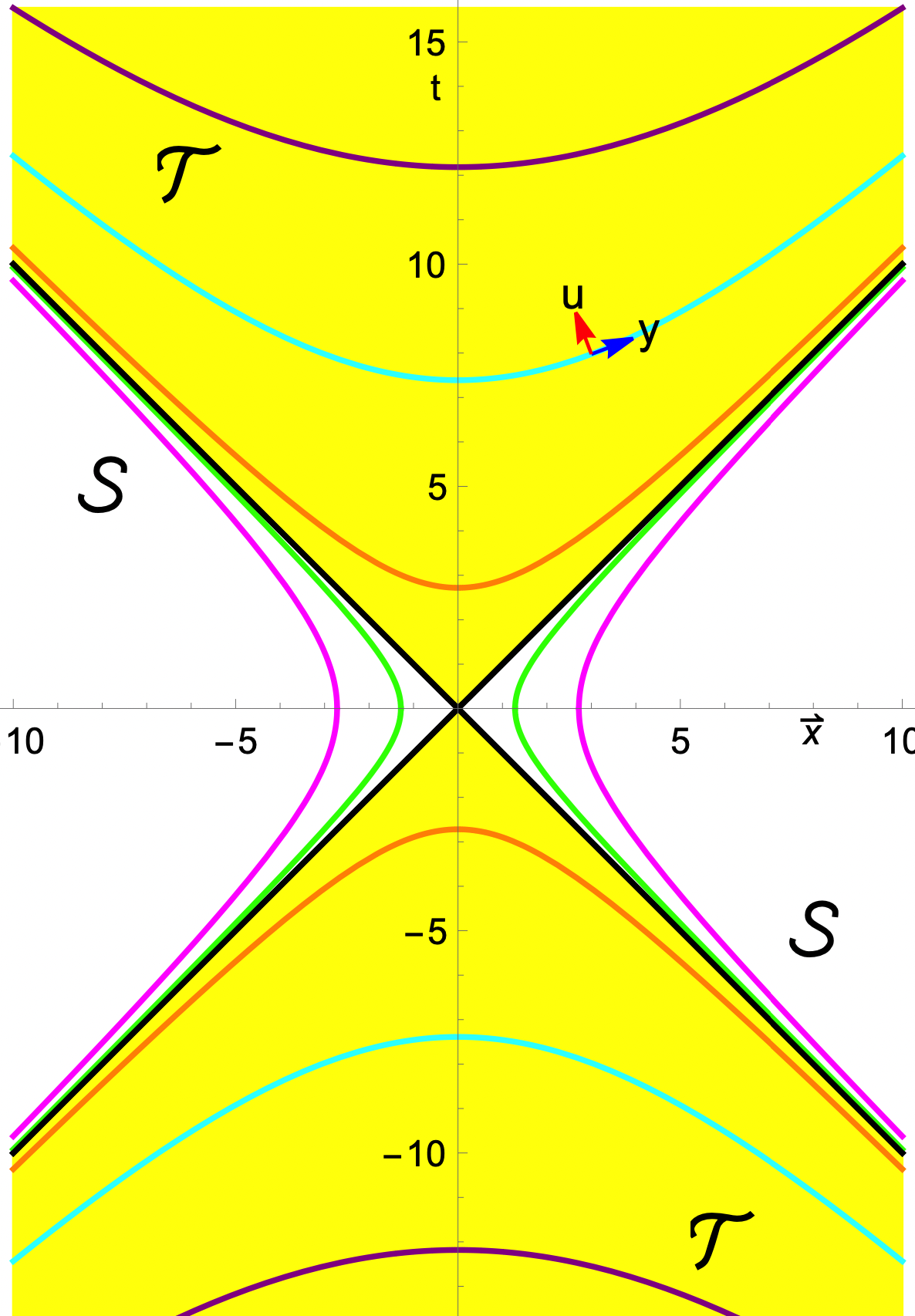
An observer sitting at center 0, could witness 4-dim spacetime foliations: 1. lightcone-interior into unit-hyperboloids `H^3` & 2. lightcone-exterior into `3`-dimensional de Sitter spaces `dS_3`; care should be taken in choosing (temporal/spatial) foliation parameter `u`, e.g. as shown on left. Moreover, the symmetric spaces `H^3` and `dS_3` are isomorphic to non-compact coset spaces built from the Lorentz group `SO(1,3)`: `H^3~=SO(1,3)//SO(3)` and `dS_3~=SO(1,3)//SO(1,2)`. Keeping this in mind and using dimensional reduction on `RRxxG//H` with gauge group `G=SO(1,3)`, we employed a `G`-invariant connection one-form `ccA` in 'temporal' guage—meaning `ccA` transforms into a single-variable field `phi(u)`, varying with `u`—to obtain analytic Yang–Mills solutions in a recent work. The resultant field equation for `phi(u)` is simply Newton's equation for an inverted double-well potential; solutions are well known Jacobi elliptic functions. The color electric- and magnetic-fields and the corresponding stress-energy tensor are singular at the lightcone, but the latter can be regularized. This work was also presented at a Colloquiium in Strasbourg [proceeding].

Lately, Daniel Friedan has tried to explain the early cosmological epoch as a coupled Einstein–Yang–Mills–Higgs system with a `SU(2)` gauge field in a conformally flat (spatialy closed) background. A `SO(4)`-symmetry is then imposed on the system that makes the Higgs field vanish. The proposal only works until the Electroweak energy scale after which `SO(4)`-symmetry is violated and the Higgs field rolls down to it's minima as shown in the figure on the left. Explicit time-dependent solutions for the scale-factor and the remaining scalar field (after the symmetry is imposed on the gauge field) are given in terms of two different sets of anharmonic oscillators. We have analysed the stability of such solutions against arbitrary linear perturbations of the gauge field in a recent work. The time-dependent eigenmodes that arise after linearising the Yang–Mills equations depend on the `fr su(2)` spin values `j` and needs to be analysed for different spin cases. We have used the Floquet analysis to study the stability behaviour of these modes for up to `j=2` and found that they are all unstable.

The study of electromagnetic knots—those EM fields whose field-lines form closed non-trivial knots like the ones shown on the left with electric (red) and magnetic (green) field lines—has been an active area of research among a section of theoretical physicists ever since Antonio F. Rañada first introduced them in 1989. Interestingly, some of these simple knot configurations, including the one with figure-eight topology, have been experimentally realized lately, using laser beams with knotted polarization singularities. A new method of constructing families of such knot solutions using a de Sitter–Minkowski conformal correspondence, while passing via a finite `S^3`-cylinder, was recently proposed that would complement the other existing methods. These basis-knot solutions, characterized by spin `j` of `S^3`-harmonics, could be used to formally expand any finite-energy, finite-action field configuration. We have studied several symmetry aspects of such basis-knot configurations like relation between energy and helicity, classification of null fields, and transport of electromagnetic flux across the Penrose diagram. We have also computed Noether charges associated with the conformal group for an arbitrary linear combinations of such basis configurations for a fixed `j`. More recently, we have analyzed the trajectories of charged particles in the background of such knotted electromagnetic field confingurations with the aid of numerical simulations.

It has long been argued that the quantum structure of spacetime is discrete and the observed classical continuum of spacetime is an emergent phenomenon. The famous models of such space(time) has a characteristic configuration-space fuzzyness, analogous to a quantum mechanical phase-space, and cures the well known issue of gravitational collapse at small length scale as proposed here. The geometry of such spaces can be studied using the spectral triple toolkit of Noncommutative geometry, developed by Field medalist Alain Connes. The distance between any pair of generalized points, technically known as pure-states, in such a setting can be computed using these spectral triples consisting of 3 mathematical objects: a non-commutative algebra, a Hilbert space and a Dirac operator. We have thoroughly investigated the geometry of two such models: the `2`-dimensional Moyal plane and the `3`-dimensional Fuzzy sphere by revising a previous calculation and providing a new, almost general, result for arbitrary spin-`j` `fr su(2)` representation of the Fuzzy sphere (a peculiar result for `j=1//2` is demonstrated on the left). Unlike others, we perform our calculations using a Hilbert–Schmidt operatorial formalism thus avoiding any issues arising from the choice of star products. We also studied another model called the doubled Moyal plane where we reproduced the "Pythagoras theorem" between different sets of pure states and demostrated the emergence of Higgs field from the internal fluctuation of the Dirac operator.